Horst-Holger Boltz
most recent e-mail address: ztlobhh@uchicago.edu
(reverse the order of the first part)
University of Chicago
James Franck Institute
currently visitor at
University of Pennsylvania
Department of Physics and Astronomy
Group of Prof. A. J. Liu
Office: David Rittenhouse Laboratory, 2N18
Employed as part of the Simons Collaboration on Cracking the Glass Problem
associated PIs: J. Kurchan, A. Liu, S. Nagel
previously:
postdoctoral researcher
Georg-August-Universität Göttingen,
Faculty of Physics,
Institute for nonlinear dynamics
Theoretical Biophysics (Prof. S. Klumpp)
email: firstname.lastname@phys.uni-goettingen.de
(grad) student
TU
Dortmund University,
Department of Physics,
T1b (Prof. J. Kierfeld)
email: firstname.lastname@udo.edu
minimal navigation:
Research
In general, I have a broad interest in problems of statistical/soft matter physics. The following is a small overview of topics in which this interest lead to a publication or might lead in the foreseeable future. This list is sorted roughly chronologically and does not intend to be scientifically rigorous. The nicer german version of this page does no longer exist, globalization takes its toll.
Semiflexible Polymers in (disordered) potentials (w/ J. Kierfeld and, partially, T.A. Kampmann)
The behaviour of elastic bodies (manifolds) in a disordered (random) medium is of interest in a multitude of ways. The simplest model, bascially a thread under tension (called directed polymer in random medium, DPRM), continues to be the subject of active research, in part due to its relevance for growth (as described by the Kardar-Parisi-Zhang (KPZ) equation) and transport (the (totally) asymmetric exclusion process, (T)ASEP) processes. From a theoretical perspective the interesting feature is the disorder-driven localization transition: given a sufficient amount of attractive spots in the disorder, the elastic body will deform such that it covers these continually suppressing thermal fluctuations.
We applied ourselves to this theme with a somewhat novel, albeit highly similar model, one of a stiff directed line. Here, not all excursions from the preferred conformation are penalised but only such leading to curvature in the line. This comes with the practical advantage that the localisation transition becomes accessible already in one dimension. Furthermore, such lines are an important model for semiflexible polymers.
One important motivation of this research is the notion that directed and stiff directed lines show identical binding criticality when appropriately shifting dimensions. That this mapping seems to hold for disorder potentials as well is an important result of our comprehensive study of the behavior of stiff directed lines in disorder. A simplifying graphic interpretation (the systematic way of doing this is the so-called replica method) is imagining the fluctuations of a line as copies of this line. In the localised that these copies are in the same state (as fluctuations are effectively frozen) and they are, thus, effectively (mediated through the external potential) bound to each other.
▾ Boltz, Kierfeld, Phys. Rev. E 86, 060102(R) (2012)
▾ Boltz, Kierfeld, Phys. Rev. E 88, 012103 (2013)
Additionally,  Depinning of a stiff directed line under force (visualized by a tilt of the energy landscape).we considered the depinning transition, i.e. the behavior under a constantly acting force. Above a finite threshold this force is dominant and the line is moving as a whole whith a friction caused by the random potential landscape it's traversing. The transition between the regmes of vanishing and finite long-time center-of-mass speed are in some regards similar to classical critical phenomena. The possible interplay of the static localization transition and the dynamic transition at a finite force threshold was of particular interest to us. It turns out that the depinning is ultimately a T=0 fixed point and temperature effects are negligible. Remarkably (and different from the static transition), this behavior is well described by functional renormalization group theory.
Depinning of a stiff directed line under force (visualized by a tilt of the energy landscape).we considered the depinning transition, i.e. the behavior under a constantly acting force. Above a finite threshold this force is dominant and the line is moving as a whole whith a friction caused by the random potential landscape it's traversing. The transition between the regmes of vanishing and finite long-time center-of-mass speed are in some regards similar to classical critical phenomena. The possible interplay of the static localization transition and the dynamic transition at a finite force threshold was of particular interest to us. It turns out that the depinning is ultimately a T=0 fixed point and temperature effects are negligible. Remarkably (and different from the static transition), this behavior is well described by functional renormalization group theory.
▾ Boltz, Kierfeld, Phys. Rev. E 90, 012101 (2013)
Several degrees more fundamental, but similar in spirit from a suitable perspective, is the adsorption of a single polymer onto a substrate. Here, the entropic penalty due to the confinement near the substrate competes with the attractive binding energy due to a short-ranged binding potential. We (primarily Tobias A. Kampmann) determined the critical potential strength as a function of the polymer's bending stiffness numerically and analytically, with good agreement of the two approaches. Both a very small and a very large bending stiffness lead to vanishing entropic costs facilitating the adsorption in these limits. In the intermediary regime, however, is a region in which the semiflexibility leads to higher (and, thus, somewhere maximal) critical strengths. Thus, one conclusion is a selectivity of adsorption with respect to bending stiffness. Another way of possibly controlling the adsorption is using a structured substrate. We studied the effect of using a substrate with finite curvature.
▾ Kampmann, Boltz, Kierfeld, J. Chem. Phys. 139, 034903 (2013)
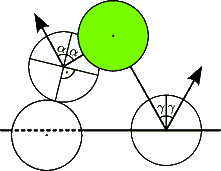
Deformable microswimmers (w/ J. Kierfeld)
As
Iterative solution to the coupled problem of elasticity and hydrodynamics part of the priority programme Microswimmers (SPP1726) of the german research foundation we attended to the deformation of elastic (micro-)capsules due to motion in a viscous fluid. We developed an iterative scheme that allows for the reduction of the coupled problem of hydrodynamics and capsule mechanics to two (relative) simple static equilibrium problems and tested it with the experimentally relevant model problem of passive sedimentation (motion in a (effective) gravitational potential).
▾ Boltz, Kierfeld, Phys. Rev. E 92: 033003 (2015)
▾ Boltz, Kierfeld, J. Eur. Phys. J. Spec. Top. 225: 2269 (201
There is more to write here and someone should to that... eventually.
Monte-Carlo Simulation of Systems with Steric Interactions (w/ J. Kierfeld and T.A. Kampmann)
In

The basic idea, changing a many degrees of freedom that are possibly distributed over a sizeable spatial volume without rejection, is transferred somewhat directly to more complex systems, but by its very nature non-trivial to parallelize. We showed that it is possible to do this such that the algorithmic gain in efficiency remains and strong scaling is achieved.
One example of a more complex system whose integration is (rather drastically) improved by using event-chain ideas, is a (nearly) athermal melt of (flexible polymers). Here, there is an additional topological interaction (and not only the steric (excluded volume) as in the disk system) as the exploration of the full conformational space asks for the creation and unraveling of entanglements. We were able to show that this explicitly well suited for the event-chain treatment if one accounts for the distinctness of particles with a new swap move leading to simulation speeds on par with state-of-the art molecular dynamics simulations.
▾ Kampmann, Boltz, Kierfeld, J. Comput. Phys. 281, 864 (2015)
▾ Kampmann, Boltz, Kierfeld, J. Chem. Phys. 143, 044105 (2015)
Physics with bacteria (w/ S. Klumpp)
There is more to write here and someone should to that... eventually.
Glassy systems under quasistatic driving (w/ A. Liu, S. Nagel, J. Kurchan)
Publications (Preprints)
| Localization transition of stiff directed lines in random media | |
|
HHB and J. Kierfeld, Phys. Rev. E 86, 060102(R) (2012) 10.1103/PhysRevE.86.060102 arXiv:1212.3203 [cond-mat.stat-mech] |
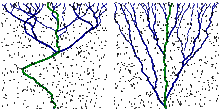 |
| We investigate the localization of stiff directed lines with bending energy by a short-range random potential. Using perturbative arguments, Flory arguments, and a replica calculation, we show that a stiff directed line in 1+d dimensions undergoes a localization transition with increasing disorder for d>2/3. We demonstrate that this transition is accessible by numerical transfer matrix calculations in 1+1 dimensions and analyze the properties of the disorder-dominated phase. On the basis of the two-replica problem, we propose a relation between the localization of stiff directed lines in 1+d dimensions and of directed lines under tension in 1+3d dimensions, which is strongly supported by identical free energy distributions. This shows that pair interactions in the replicated Hamiltonian determine the nature of directed line localization transitions with consequences for the critical behavior of the Kardar-Parisi-Zhang (KPZ) equation. Furthermore, we quantify how the persistence length of the stiff directed line is reduced by disorder. | |
| Stiff directed lines in random media | |
|
HHB and J. Kierfeld, Phys. Rev. E 88, 012103 (2013) 10.1103/PhysRevE.88.012103 arXiv:1306.4795 [cond-mat.stat-mech] |
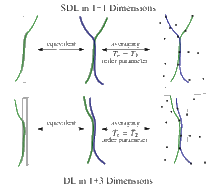 |
| We investigate the localization of stiff directed lines with bending energy by a short-range random potential. We apply perturbative arguments, Flory scaling arguments, a variational replica calculation, and functional renormalization to show that a stiff directed line in 1+d dimensions undergoes a localization transition with increasing disorder for d>2/3. We demonstrate that this transition is accessible by numerical transfer matrix calculations in 1+1 dimensions and analyze the properties of the disorder-dominated phase in detail. On the basis of the two-replica problem, we propose a relation between the localization of stiff directed lines in 1+d dimensions and of directed lines under tension in 1+3d dimensions, which is strongly supported by identical free-energy distributions. This shows that pair interactions in the replicated Hamiltonian determine the nature of directed line localization transitions with consequences for the critical behavior of the Kardar-Parisi-Zhang equation. We support the proposed relation to directed lines via multifractal analysis, revealing an analogous Anderson transition-like scenario and a matching correlation length exponent. Furthermore, we quantify how the persistence length of the stiff directed line is reduced by disorder. | |
| Controlling adsorption of semiflexible polymers on planar and curved substrates | |
|
T.A. Kampmann, HHB and J. Kierfeld, J. Chem. Phys. 139, 034903 (2013) 10.1063/1.4813021 arXiv:1306.4844 [cond-mat.soft] supplemental material |
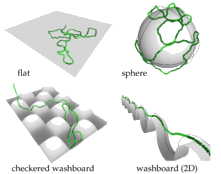 |
| We study the adsorption of semiflexible polymers such as polyelectrolytes or DNA on planar and curved substrates, e.g., spheres or washboard substrates via short-range potentials using extensive Monte Carlo simulations, scaling arguments, and analytical transfer matrix techniques. We show that the adsorption threshold of stiff or semiflexible polymers on a planar substrate can be controlled by polymer stiffness: adsorption requires the highest potential strength if the persistence length of the polymer matches the range of the adsorption potential. On curved substrates, i.e., an adsorbing sphere or an adsorbing washboard surface, the adsorption can be additionally controlled by the curvature of the surface structure. The additional bending energy in the adsorbed state leads to an increase of the critical adsorption strength, which depends on the curvature radii of the substrate structure. For an adsorbing sphere, this gives rise to an optimal polymer stiffness for adsorption, i.e., a local minimum in the critical potential strength for adsorption, which can be controlled by curvature. For two- and three-dimensional washboard substrates, we identify the range of persistence lengths and the mechanisms for an effective control of the adsorption threshold by the substrate curvature. | |
| Depinning of stiff directed lines in random media | |
|
HHB and J. Kierfeld, Phys. Rev. E 90, 012101 (2013) 10.1103/PhysRevE.90.012101 arXiV: 1406.4270 [cond-mat.stat-mech] |
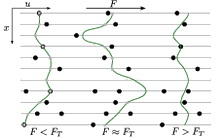 |
| Driven elastic manifolds in random media exhibit a depinning transition to a state with nonvanishing velocity at a critical driving force. We study the depinning of stiff directed lines, which are governed by a bending rigidity rather than line tension. Their equation of motion is the (quenched) Herring-Mullins equation, which also describes surface growth governed by surface diffusion. Stiff directed lines are particularly interesting as there is a localization transition in the static problem at a finite temperature and the commonly exploited time ordering of states by means of Middleton's theorems [Phys. Rev. Lett. 68, 670 (1992)] is not applicable. We employ analytical arguments and numerical simulations to determine the critical exponents and compare our findings with previous works and functional renormalization group results, which we extend to the different line elasticity. We see evidence for two distinct correlation length exponent | |
| Parallelized event chain algorithm for dense hard sphere and polymer systems | |
|
T.A. Kampmann, HHB and J. Kierfeld, J. Comput. Phys. 281, 864 (2015) 10.1016/j.jcp.2014.10.059 arXiv:1409.6948 [cond-mat.stat-mech] |
 |
| We combine parallelization and cluster Monte Carlo for hard sphere systems and present a parallelized event chain algorithm for the hard disk system in two dimensions. For parallelization we use a spatial partitioning approach into simulation cells. We find that it is crucial for correctness to ensure detailed balance on the level of Monte Carlo sweeps by drawing the starting sphere of event chains within each simulation cell with replacement. We analyze the performance gains for the parallelized event chain and find a criterion for an optimal degree of parallelization. Because of the cluster nature of event chain moves massive parallelization will not be optimal. Finally, we discuss first applications of the event chain algorithm to dense polymer systems, i.e., bundle-forming solutions of attractive semiflexible polymers. | |
| Shapes of Sedimenting Soft Elastic Capsules in a Viscous Fluid | |
|
HHB and J. Kierfeld, Phys. Rev. E 92, 033003 (2015) (selected as Editors' suggestion) 10.1103/PhysRevE.92.033003 arXiv: 1509.02390[cond-mat.soft] |
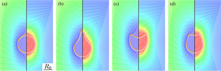 |
| Soft elastic capsules which are driven through a viscous fluid undergo shape deformation coupled to their motion. We introduce an iterative solution scheme which couples hydrodynamic boundary integral methods and elastic shape equations to find the stationary axisymmetric shape and the velocity of an elastic capsule moving in a viscous fluid at low Reynolds numbers. We use this approach to systematically study dynamical shape transitions of capsules with Hookean stretching and bending energies and spherical rest shape sedimenting under the influence of gravity or centrifugal forces. We find three types of possible axisymmetric stationary shapes for sedimenting capsules with fixed volume: a pseudospherical state, a pear-shaped state, and buckled shapes. Capsule shapes are controlled by two dimensionless parameters, the Föppl-von-Kármán number characterizing the elastic properties and a Bond number characterizing the driving force. For increasing gravitational force the spherical shape transforms into a pear shape. For very large bending rigidity (very small Föppl-von-Kármán number) this transition is discontinuous with shape hysteresis. The corresponding transition line terminates, however, in a critical point, such that the discontinuous transition is not present at typical Föppl-von-Kármán numbers of synthetic capsules. In an additional bifurcation, buckled shapes occur upon increasing the gravitational force. This type of instability should be observable for generic synthetic capsules. All shape bifurcations can be resolved in the force-velocity relation of sedimenting capsules, where up to three capsule shapes with different velocities can occur for the same driving force. All three types of possible axisymmetric stationary shapes are stable with respect to rotation during sedimentation. Additionally, we study capsules pushed or pulled by a point force, where we always find capsule shapes to transform smoothly without bifurcations. | |
| Monte Carlo Simulation of Dense Polymer Melts Using Event Chain Algorithms | |
|
T.A. Kampmann, HHB and J. Kierfeld, J. Chem. Phys. 143, 044105 (2015) 10.1063/1.4927084 arXiv:1502.06447 [cond-mat.soft] |
 |
| We propose an efficient Monte Carlo algorithm for the off-lattice simulation of dense hard sphere polymer melts using cluster moves, called event chains, which allow for a rejection-free treatment of the excluded volume. Event chains also allow for an efficient preparation of initial configurations in polymer melts. We parallelize the event chain Monte Carlo algorithm to further increase simulation speeds and suggest additional local topology-changing moves (“swap” moves) to accelerate equilibration. By comparison with other Monte Carlo and molecular dynamics simulations, we verify that the event chain algorithm reproduces the correct equilibrium behavior of polymer chains in the melt. By comparing intrapolymer diffusion time scales, we show that event chain Monte Carlo algorithms can achieve simulation speeds comparable to optimized molecular dynamics simulations. The event chain Monte Carlo algorithm exhibits Rouse dynamics on short time scales. In the absence of swap moves, we find reptation dynamics on intermediate time scales for long chains. | |
| Stationary shapes of deformable particles moving at low Reynolds numbers | |
|
HHB and J. Kierfeld, J. Eur. Phys. J. Spec. Top. 225, 2269 (2016) 10.1063/1.4927084 arXiv:1502.06447 [cond-mat.soft] |
|
| We introduce an iterative solution scheme in order to calculate stationary shapes of deformable elastic capsules which are steadily moving through a viscous fluid at low Reynolds numbers. The iterative solution scheme couples hydrodynamic boundary integral methods and elastic shape equations to find the stationary axisymmetric shape and the velocity of an elastic capsule moving in a viscous fluid governed by the Stokes equation. We use this approach to systematically study dynamical shape transitions of capsules with Hookean stretching and bending energies and spherical resting shape sedimenting under the influence of gravity or centrifugal forces. We find three types of possible axisymmetric stationary shapes for sedimenting capsules with fixed volume: a pseudospherical state, a pear-shaped state, and buckled shapes. Capsule shapes are controlled by two dimensionless parameters, the Föppl-von-Kármán number characterizing the elastic properties and a Bond number characterizing the driving force. For increasing gravitational force the spherical shape transforms into a pear shape. For very large bending rigidity (very small Föppl-von-Kármán number) this transition is discontinuous with shape hysteresis. The corresponding transition line terminates, however, in a critical point, such that the discontinuous transition is not present at typical Föppl-von-Kármán numbers of synthetic capsules. In an additional bifurcation, buckled shapes occur upon increasing the gravitational force. | |
Teaching
The purpose of this section is personal bookkeeping and therefore motivation for translation or simply maintaining is limited. Bis einschließlich SS 2013 zusammen mit E.T.A. Kampmann, bis einschließlich WS 2014/15 an der TU Dortmund, dann an der Georg-August-Universität Göttingen. Die Auflistung hat persönlichen statistischen Wert, die Links auf die Vorlesungsseiten sind naturgemäß im Zweifel nicht persistent und werden nicht gepflegt.
| WS 2009/10 | Physik I (Profes. Khan and Kierfeld) |
| SS 2010 | Physik II (Profes. Khan and Kierfeld) |
| WS 2010/11 | Thermodynamik und Statistik (Prof. Kierfeld) |
| SS 2011 | Computational Physics (Prof. Kierfeld) |
| WS 2011/12 | Physik I (Profes. Betz, Kierfeld und Westphal, Dr. Schmidt) |
| SS 2012 | Physik II (Profes. Betz, Kierfeld und Westphal, Dr. Schmidt) |
| WS 2012/13 | Thermodynamik und Statistik (Prof. Kierfeld) |
| SS 2013 | Computational Physics (Prof. Kierfeld) |
| WS 2013/14 | Thermodynamik und Statistik (Prof. Stolze) |
| SS 2014 | Höhere Quantenmechanik (Prof. Anders) |
| WS 2014/15 | Thermodynamik and Statistik (Prof. Anders) |
| SS 2016 | Quantenmechanik I (Prof. Klumpp) (Organisation der Übung, Gestaltung der Aufgaben) |
| SS 2017 | zwei mitbetreute Bachelorarbeiten (J. Kühn, P. Simon) zur Simulation aktiver Teilchen in komplexen Geometrien/Flüssen (Prof. Klumpp) |